Shading
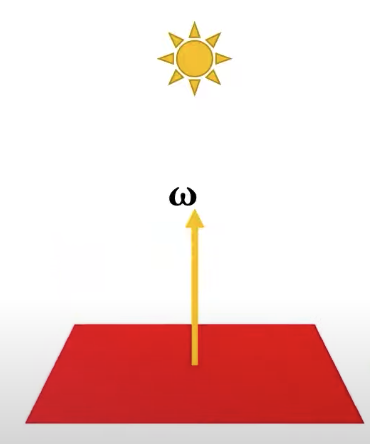
 | 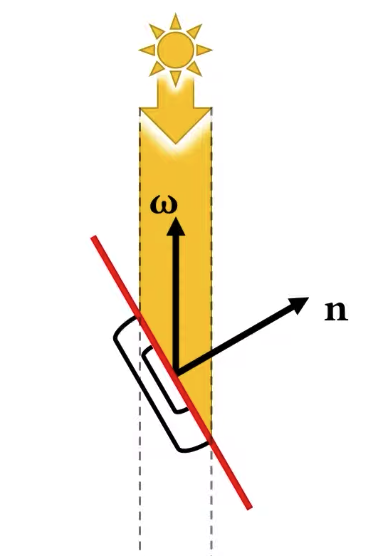 |
The same beam of light was illuminating some area on that surface, now it is illuminating and spread over a larger area on that surface. So the same amount of light is now spread over a larger area on that surface, and that’s reason why we are going to be getting less light per unit area.
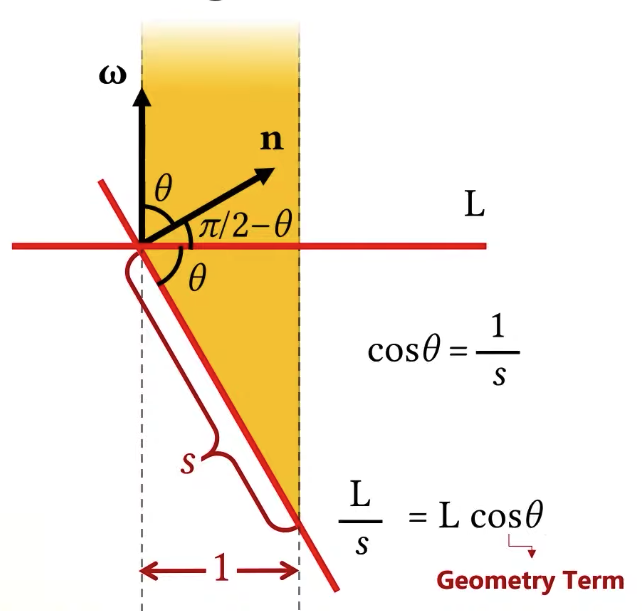
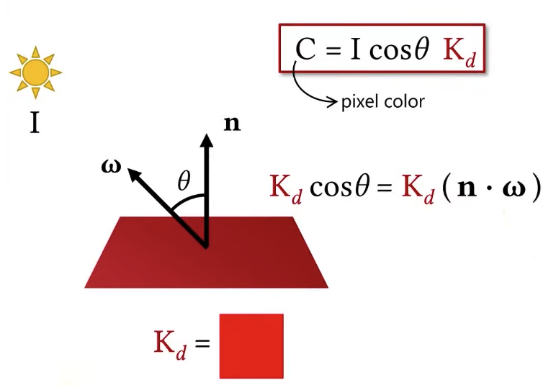
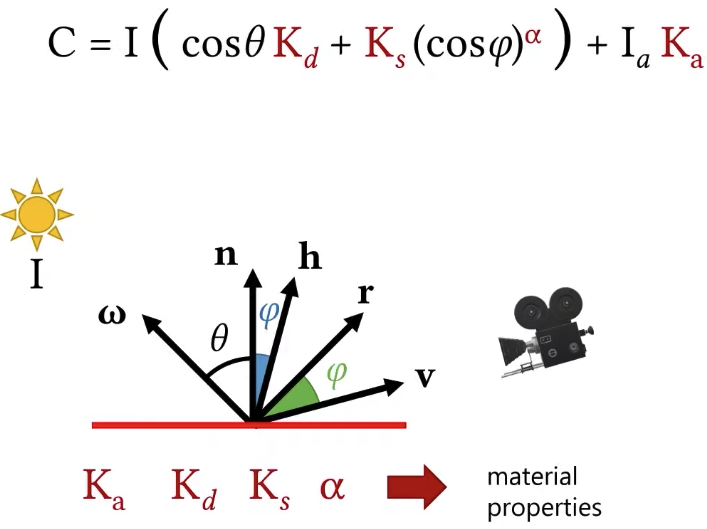
L/s, means the amount of light L spreads over s. cos(θ) will tell use the amount of light I am receiving per unit are.
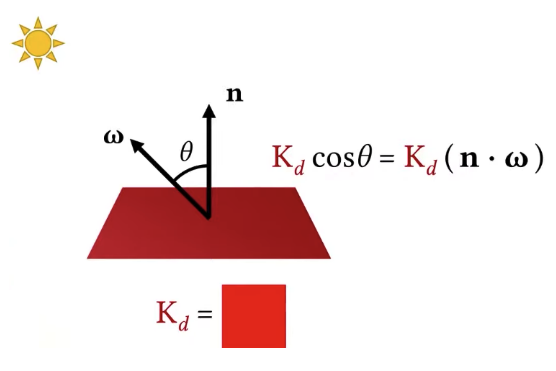
The amount of light I am receiving on the surface is going to be scaled by this angle θ. Let’s say for this case, my surface color is red, what the color I am seeing on the surface is Kdcos(θ). Since cos(θ) = n • ω if n and ω are unit vectors. Kdcos(θ) = Kd(n • w). Of course, the color also depends on the light intensity I. So the final color I am going to see on the surface is going to depend on the light intensity, the geometry term and the color of the surface.
Lambertian (Diffuse) Material
 |  |
The Lambertian material or the diffuse material is the simplest material we can think of. The entire material property is defined by a single color value. It looks OK but not appealing.

Phong Specular Reflections
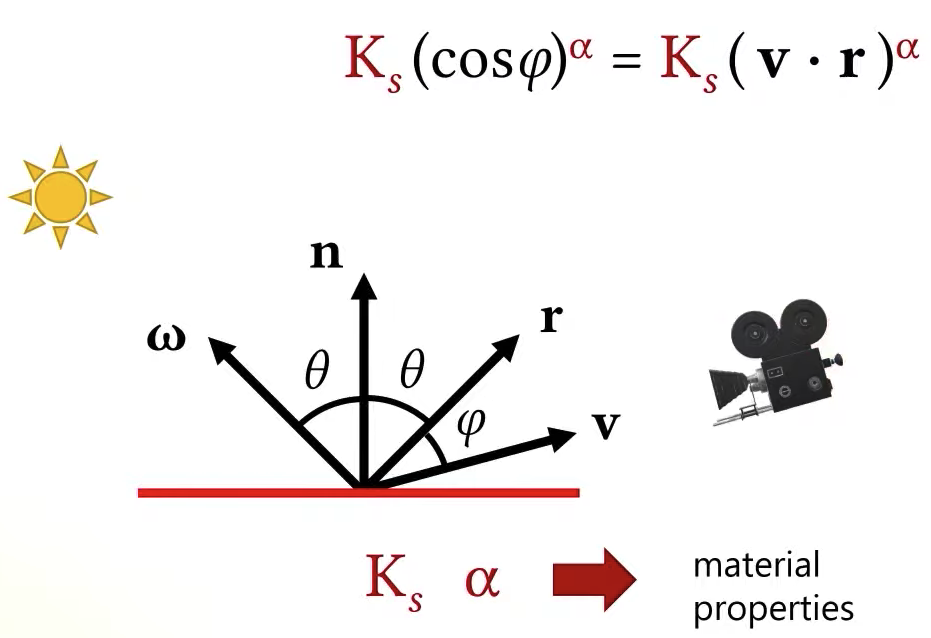
The total amount of specular illumination that I will see at that point of course will also depend on the intensity of incoming light.
Typically, materials defined by this phong model will also have a diffuse component, so there’s going to be a diffuse like lambertian component and on top of that is going to be a specular reflection. So we can add these two together, the reason why we are doing this way is that you can think about it this way, light that comes to that surface, a percentage of that light is going to reflect diffusely, very much like a lambertian material, so it’s going to reflect in all directions, equal amount, and a part of that is going to reflect specularly, and that’s going to be defined by the phong specular reflection model. So that I can write the total color I see with the phong material model like so.
Phong Material Model
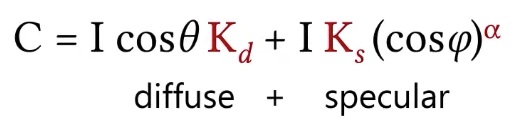
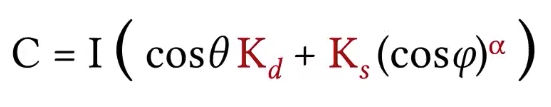
But there is a little bit of confusing part here. Remember this cosine theta is the geometry term, it has nothing to do with this diffuse part, it just determines the amount of light I am receiving per area on the surface, this is not specific to the diffuse, it should be really outside of this parentheses.
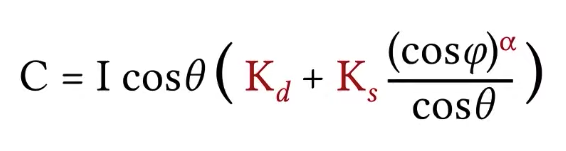
But actually you can write it in a simpler form by omitting the cosine term.
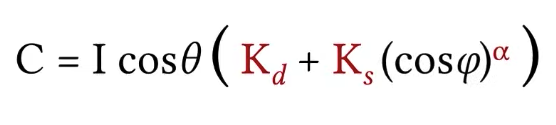
Another thing needs to know, this is actually sort of simplified representation. When you are implementing it, you need to be careful about one thing here that is the cosine theta can be negative. How can it be negative? If the light is coming behind the surface, then we shouldn’t get any illumination on surface. So a more proper way to write this would be like this:
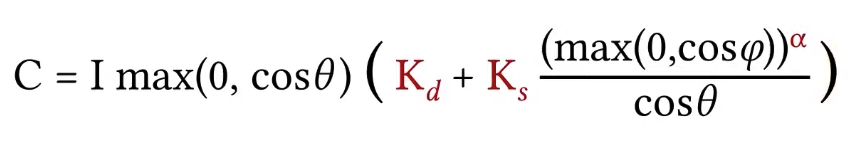
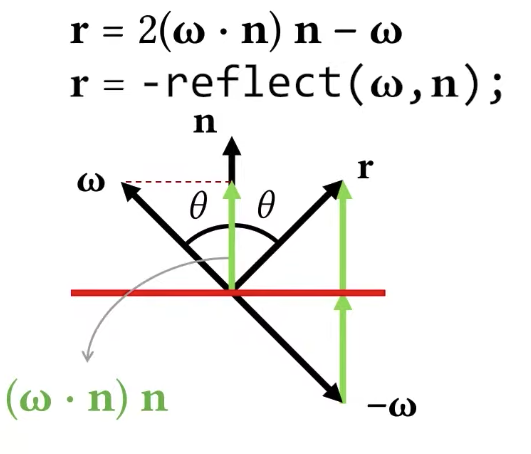
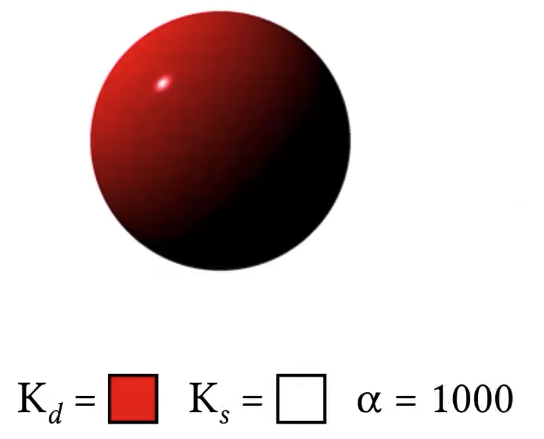
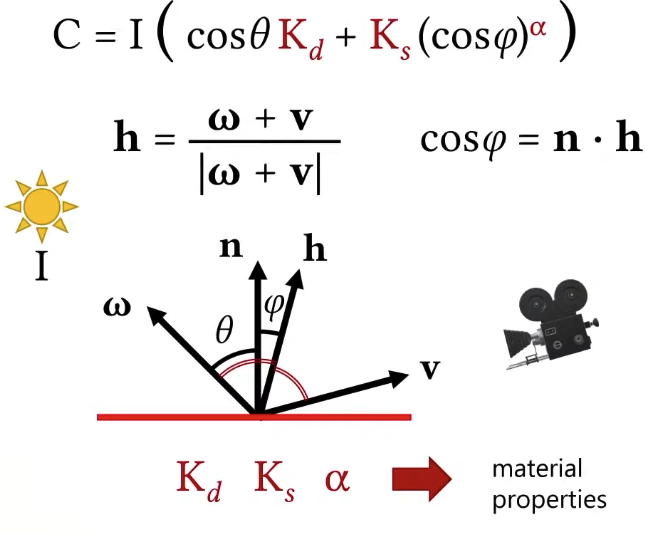
Blinn Material Model
This is not the only material model. Blinn improved this model a little bit, his material model is very similar but slightly different which makes small but important difference, so the Blinn material model does not look at the perfect reflection direction, instead, it looks at the direction that we call the half vector. The half vector is going to be half way between this light direction ω and the view direction v. It’s going to define this phi angle as the angle between the surface normal and the half vector. So that’s the only difference, everything else is exactly the same.
Blinn vs Phong Material Model
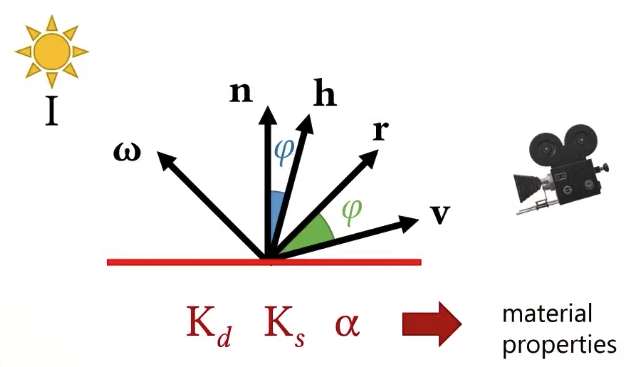 | 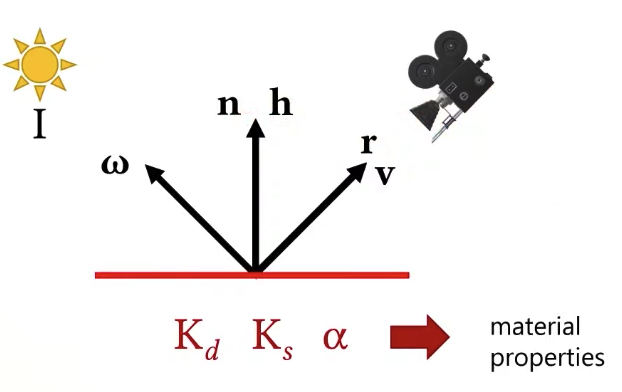 |
But remember that we are actually trying to render in 3D surfaces, we are just looking at cross section here then in this case all of the vectors are on the same plane, but in 3D they don’t have to be, light, view and normal could be in different planes, in that case actually what happens is that with this Blinn material model the shape of specular lope changes, so if you were to compare blinn and phong, the same material parameters will not give you a specular highlight of the same size, it’s also not going to give you a specular highlight of the same shape, the shape is slightly different.
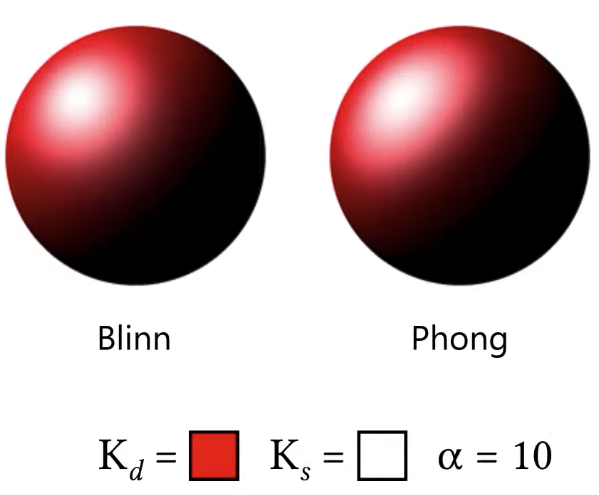 | 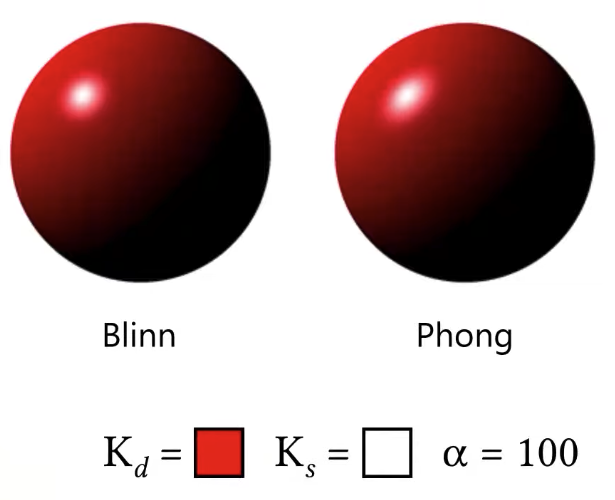 |
Blinn/Phong Material Model
These are not the most realistic models, there are a lot of more realistic materials we have today. Blinn/Phong model is still used but not as commonly used in practice. This is really a very simple material model and it works really well actually, it’s been used for decades. Today people prefer more newer more physically based material models and there are good reasons for picking and using more realistic material models.
Lighting
| Directional Light | Point Light | Spot Light |
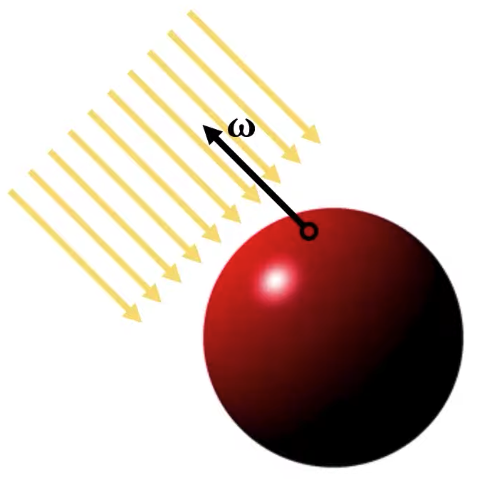 | 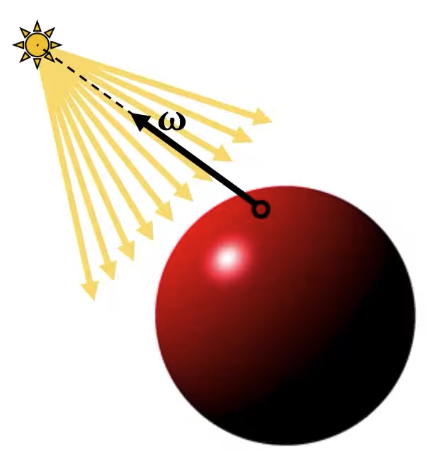 | 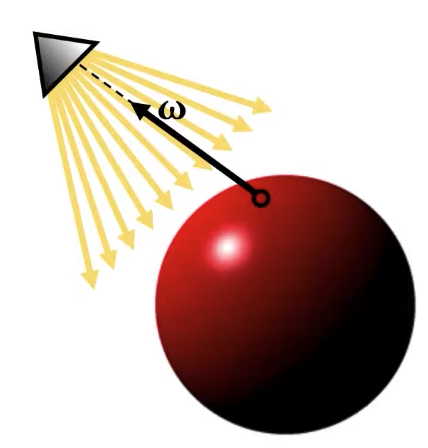 |
| Intensity Direction | Intensity Position | Intensity Position Spot light is very much like a point light source, but it has a limited angle through which it’s emitting light. |
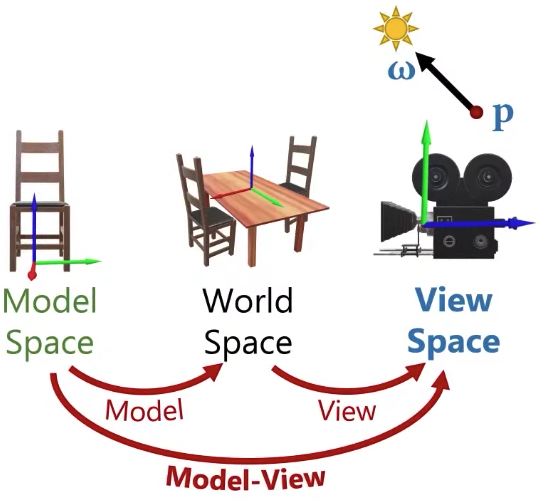
Shading Transformations
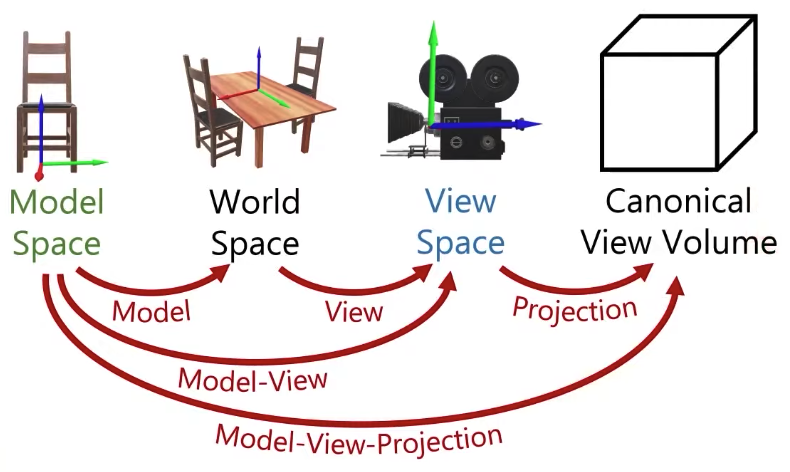
We are going to compute shading, we are going to compute some angles between vectors, so we’re going to do dot product of vectors. To be able to do anything with two vectors is that, the first thing we need to make sure is that they need to be in the same space, you can not do anything with two vectors that are in two different spaces.
For that, I need to pick a space. The canonical view volume, it’s a nice space, but it can include some non-uniform scale, and it can have perspective projection stuff, so this is not a nice space to compute angles between vectors because things are sort of deformed if I have perspective projection, so let’s get rid of this one.
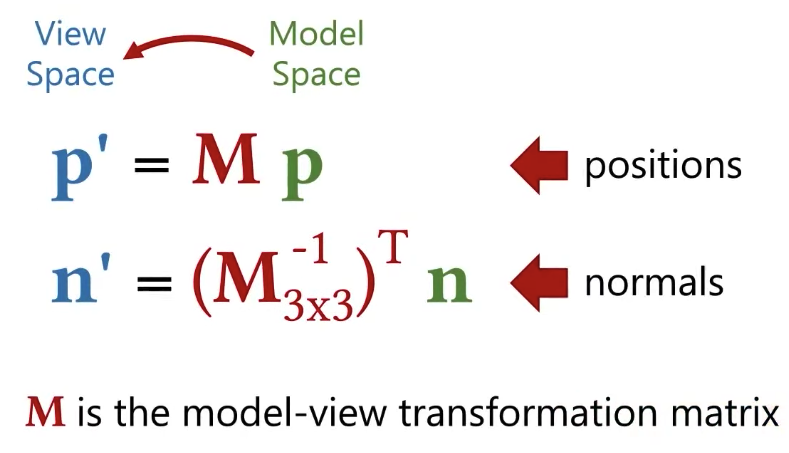
I can do shading in model space, or world space or view space. People often prefer to do shading in view space. And the reason for that is that I need the view direction to compute the specular reflections, the view direction I can easily compute it in the view space because the shading position of an object in view space is also the direction from the camera to that position.
So let’s use view space. That means I am going to have to transform everything into the view space. So if my light direction is defined in world space, I need to transform it to view space.
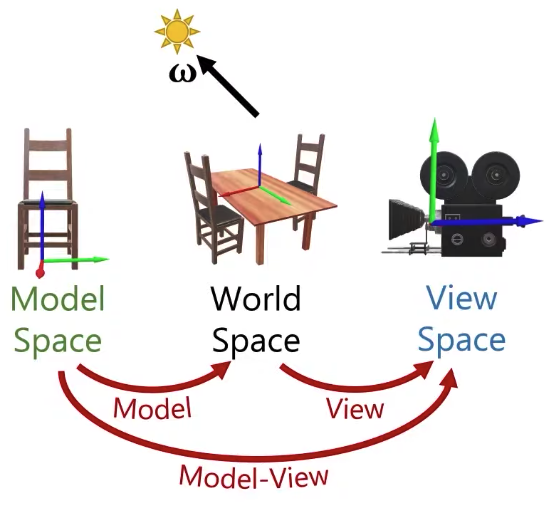 |  |
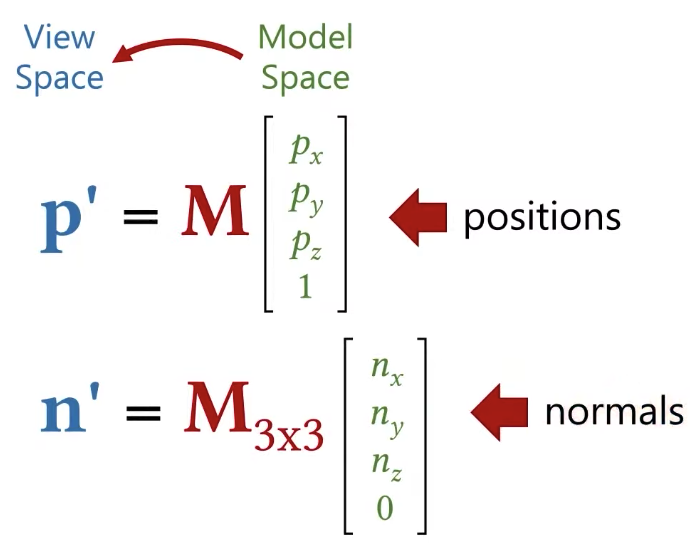
What else? I also need the surface normal. The surface normal is going to be defined in the model space, more specifically, I am going to have a surface normal per vertex defined. And I am going to have to transform that surface normal from the model space all the way to the view space.
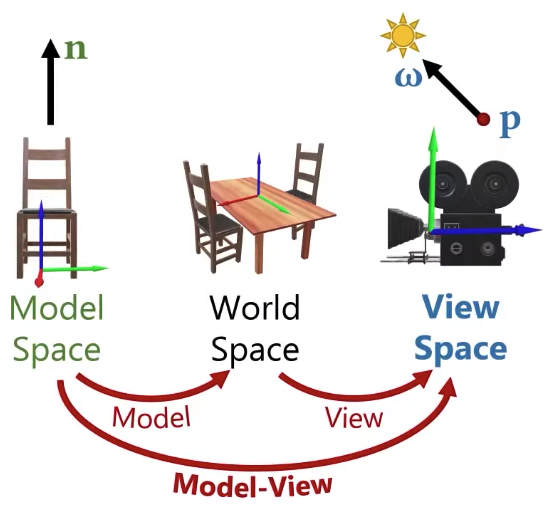 | 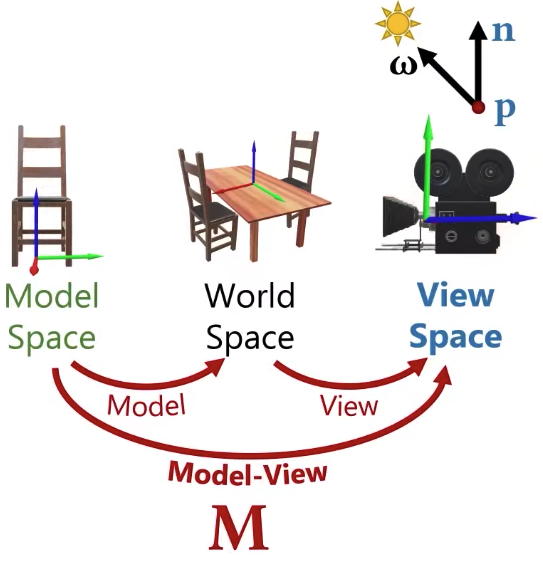 |
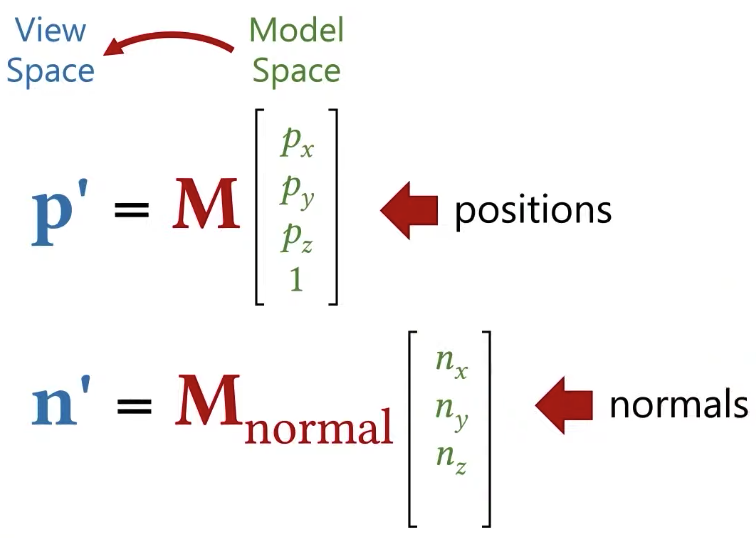
Next, what I am going to do is to transform my object model properties like position, normal to the view space.
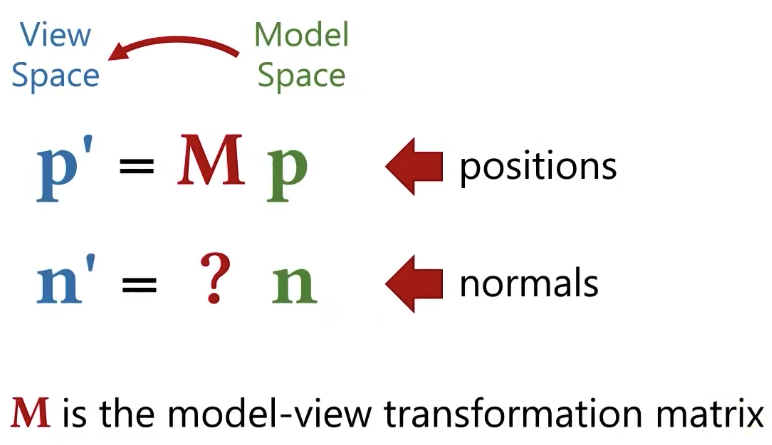
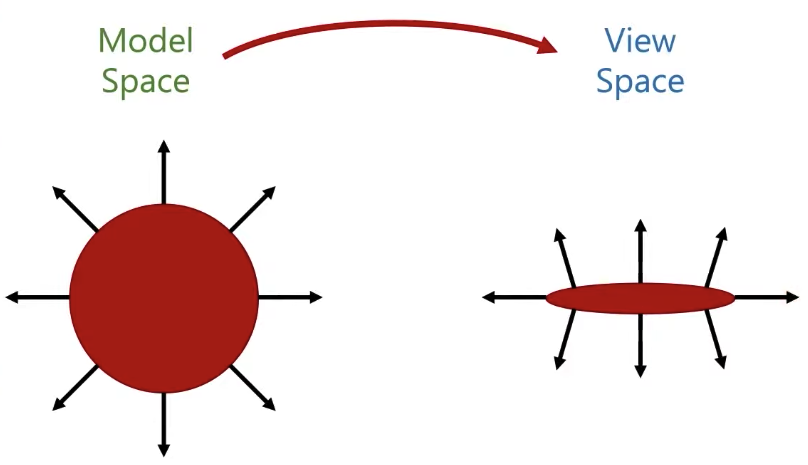
I can do the transformation for positions easily by multiple the matrix, but can I simply do that for normals as well? The answer is NO.
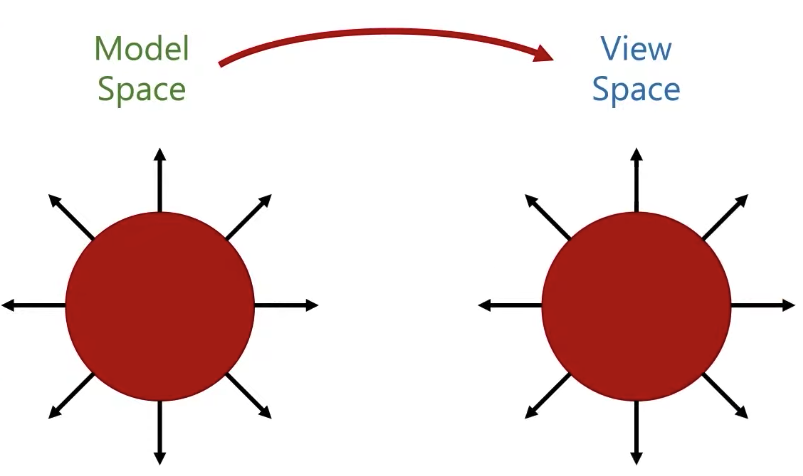 | 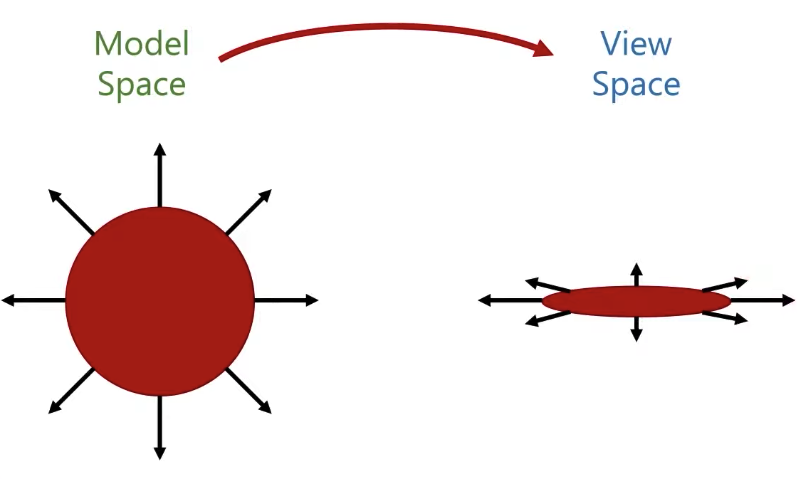 |
What I need actually is to apply the opposite of that scale, and if I do that, what I am going to get is a vector that’s going to be perpendicular to the surface normal.
 |  |
We can calculate the R2, S and R1 by SVD decomposition, but it is a little bit too complex, we can just use the matrix properties in linear algebra.
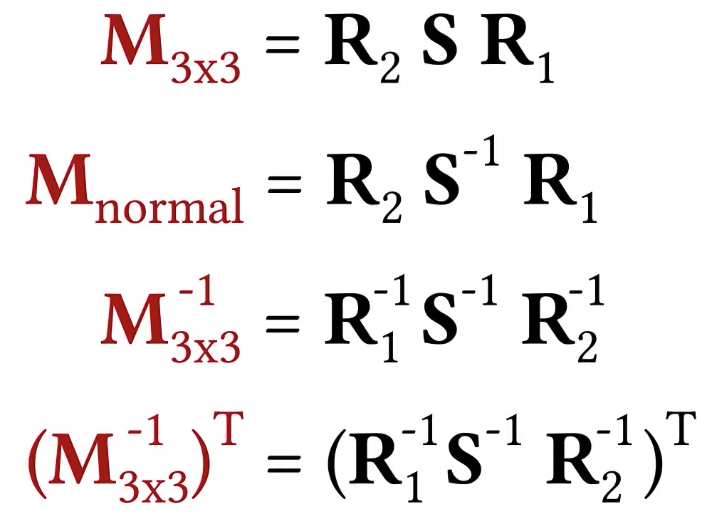 |  | 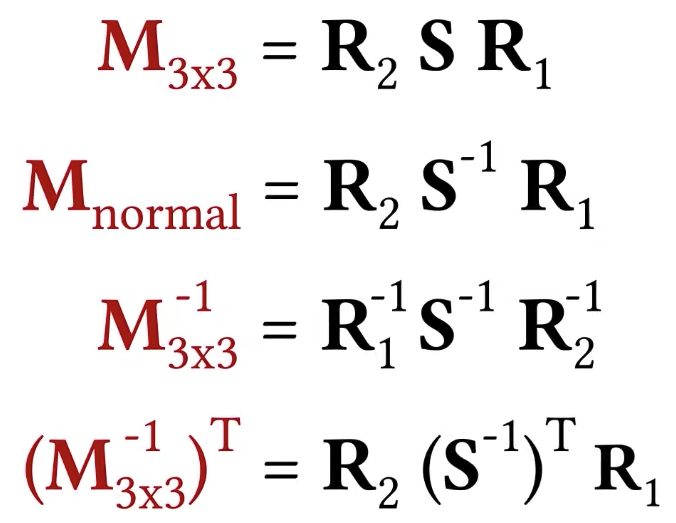 |
Gouraud Shading
The legacy OpenGL was designed to do Gouraud shading. Its basic idea is that for shading a triangle, what I do is that for each one of those vertices, I can do shading based on the surface normal here defined at this vertex, I can do shading and compute a color for each one of these three vertices. Then I can interpolate the color value here on the triangle and find the color value at any point on this triangle using barycenters coordinates.
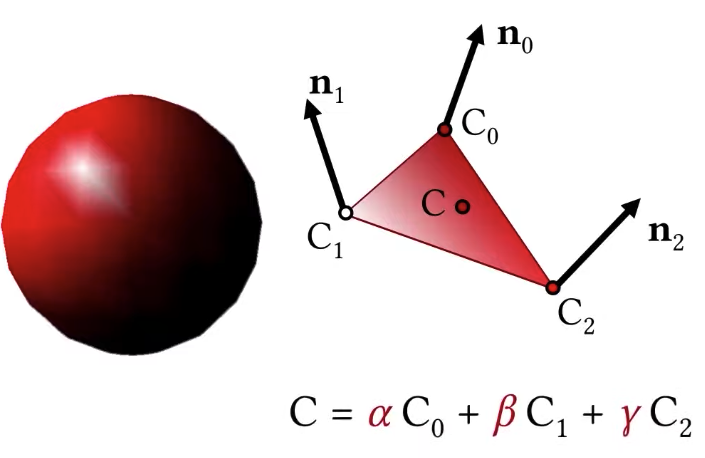 |  |
Phong Shading
Don’t mix this with Phong material model. It’s slightly different concept. Regardless of what materials you use, we do phong shading here. For computing the color at any point on that triangle, what I am going to do is to interpolate the surface normals, but we’re not going to do that in the graphics rendering pipeline ourselves, the rasterizer will do this for us. It’s going to interpolate the surface normals we send to the rasterizer as our vertex attribute, when you output the surface normal from your vertex shader, it’s going to pass the rasterizer and the rasterizer will send the interpolated value to your fragment shader.

So, finally.

Model-view and model-view-projection matrices are supposed to be 4×4 matrices. Model-view for normal matrix is supposed to be 3×3 matrix.
The positions and the transforms I computed will arrive at the fragment shader all interpolated. So I am going to have the position and normal inside my fragment shader. I also need the light direction. So I can send my light direction to my fragment shader as a uniform value. A question is that which space should I use for representing that uniform value? Obviously it has to be the same space, I am doing shading in the view space, so my light direction I am sending to my fragment shader must be in the view space as well. A follow up question is that should I transform my direction to view space by multiplying it with the view matrix inside the fragment shader? Absolutely NO. Because I don’t want to do the same computation every time my fragment shader is executed. If I need to transform my light direction to the view space, I need to do that once, I can do that on the CPU, and send it to my fragment shader.
A fragment shader code sample:
#version 330 core
out vec4 FragColor;
in VS_OUT {
vec3 FragPos;
vec3 Normal;
vec2 TexCoords;
} fs_in;
uniform sampler2D floorTexture;
uniform vec3 lightPos;
uniform vec3 viewPos;
uniform bool blinn;
void main()
{
vec3 color = texture(floorTexture, fs_in.TexCoords).rgb;
// ambient
vec3 ambient = 0.05 * color;
// diffuse
vec3 lightDir = normalize(lightPos - fs_in.FragPos);
vec3 normal = normalize(fs_in.Normal);
float diffWeight = max(0.0, dot(lightDir, normal);
vec3 diffuse = diffWeight * color;
// specular
vec3 viewDir = normalize(viewPos - fs_in.FragPos);
vec3 reflectDir = reflect(-lightDir, normal);
float spec = 0.0;
if (blinn)
{
vec3 halfwayDir = normalize(lightDir + viewDir);
spec = pow(max(0.0, dot(normal, halfwayDir)), 32.0);
}
else
{
spec = pow(max(0.0, dot(viewDir, reflectDir)), 8.0);
}
vec3 specular = spec * vec3(0.3); // assume bright white light color
FragColor = vec4(ambient + diffuse + specular, 1.0);
}[Note: Primary contents come from Professor Cem Yuksel’s Interactive Graphics course, check out his website for more details]

